A simple drum model, where the vibration of the lower membrane is activated by the strike on the upper membrane. Notice the delay in the movement of the lower membrane.
Two important features involved in this process of embedding are
• the air/structure coupling
• the boundary conditions over the walls of the 3D enclosure
The coupling between the system and the air is fundamental in reproducing the acoustic field that is generated by the excitation of the structure. The behaviour of the structure and the surrounding air is, in fact, strongly correlated, with the two components continuously interacting with one another in the real world. Hence the need to implement suitable coupling conditions to allow this exchange of energy to happen.
As the 3D enclosure that can be simulated is obviously limited, numerical techniques must be employed in order to specify the behaviour of the acoustic field over the outer boundaries of the region. When simulating a real room, a complex theoretical model must be adopted in order to capture the properties of the different materials with which the acoustic waves interact. A simpler, but by no means trivial case is that of an infinite space, where the acoustic waves, after being generated, travel unimpeded towards infinity. Here, the outer boundary of the embedding region must be made acoustically transparent, by applying suitable numerical absorbing conditions.
Radiation pattern of a 3D embedded drum.
As the dimension of the system and the number of interacting components increase, the numerical code can become more and more computationally expensive. In this case, the use of parallel computation and GPUs can be helpful.
Timpani
One of the first 3D instruments that have been simulated in the NESS Project are timpani drums. The presence of a single membrane makes them a relatively simple system to tackle, although the exact shape of the cavity can present some difficulties from the modelling side.
The basic model consists of a shell, generally circularly symmetric, but of a curved dome-like shape. A single membrane is tensioned across the top, and the membrane is in contact with a 3D acoustic field both inside the drum cavity, and external to the drum.
As far as simulation goes, in a time domain implementation, the air and membranes must be represented on distinct grids—generally, for good quality synthesis, one needs to tailor the grid to the particular component. This means that at the air/membrane interface, some form of interpolation between the two grids is necessary, and the coupling needs to obey continuity laws for pressure and velocity. At the rigid shell boundary, a zero normal velocity condition is enforced—which is a convenient assumption, but not entirely true, as the shell possesses its own dynamics!
Here are some sounds obtained with this model:
One timpani roll
Timpani hits
One timpani pattern
It is possible to embed several of these instruments in the same room, and create complex musical gestures. For example:
Two timpani hits
Three timpani hits
Four timpani hits
The following video illustrates the interaction of four different timpani drums embedded in an anechoic space.
You can read about our numerical timpani drum model here.
This short conference proceedings article was expanded into an article in the Journal of the Audio Engineering
S. Bilbao and C. J. Webb. Physical Modeling of Timpani Drums in 3D on GPGPUs, Journal of the Audio Engineering Society, 61(10):737-748, 2013.
3D Plate Environment
Modular instruments are an attractive option for sound synthesis, and several different environments have been proposed in the past. One of the possibilities when working with instruments embedded in 3D is to place several of them in the same “box” and let them interact.
This is what has been done with the Multiplate 3D code. In this system, several plates, described by nonlinear (von Kármán) equations, can be placed within the same box of air, with which they interact. The user can specify all the parameters of the plates, including the size and the position. The output sound can be taken at many points simultaneously within the box. This is how a typical system looks like (red dots are output locations):
 Diagram of a typical 3D plate environment.
Diagram of a typical 3D plate environment.
Here are a few sounds obtained with this system:
|
| Gesture on five plates |
|
Roll on three plates |
It is possible to play with the dimension of the system, and create very big instruments that are not commonly encountered in the real world. This is a simulation of a 2 metre square gong!
References
[1] A. Torin and S. Bilbao. A 3D Multi-Plate Environment for Sound Synthesis, Proceedings of the 16th International Digital Audio Effects Conference, Maynooth, Ireland, Sept. 2013.
[2] A. Torin. Percussion instrument modelling in 3D: Sound synthesis through time domain numerical simulation, Ph.D. Thesis, University of Edinburgh, 2016.
Snare Drums
The snare drum is a complex instrument, as it involves several interacting components. The basic design is simple, consisting of two membranes stretched across a cylindrical shell: one which is struck by the player (the batter head), and another passive membrane (the carry head). Whereas in some double-membrane drums the role of the second membrane is relatively minor, in the case of the snare drum it is dominant. The carry head is connected to a set of loosely tensioned wires (the snares), stretched across it, and which vibrate sympathetically to vibrations transmitted from the batter head through the drum cavity. The resulting timbre is unpitched, and almost completely noise-like.
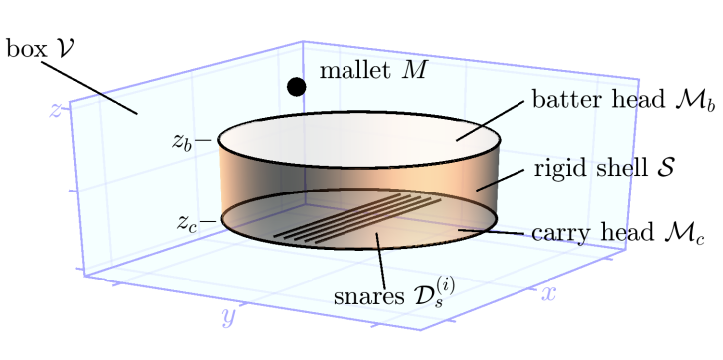 Snare drum model with the various components.
Snare drum model with the various components.
The simulation of the snare drum has been tackled by the PI a few years ago [1]. Here are a few sound examples:
[Please download the file below.]
MP4 format | Ogg format
[Please download the file below.]
MP4 format | Ogg format
[Please download the file below.]
MP4 format | Ogg format
During the Project, the collisions between the mallet and the upper membrane were included in the model. This, together with the interaction between the snares and the carry membrane, have been implemented using a novel, energy conserving approach for modelling contact dynamics. See [2,3,4] for more details on the method.
As shown on the video below, when a mallet (modelled as a lumped object) strikes the upper membrane, a positive pressure is generated inside the cavity, which pushes downwards the carry head and the snares. When the snares reach their maximum displacement, they start to move upwards, until they collide with the carry membrane, which by that time is moving downwards. After this first bounce, the movements of the snares become rapidly randomised. In the lossless case, the total energy of the system is conserved, and variations can only be observed in the last digits of the energy value (machine accuracy). The energy plot shows how the initial energy of the mallet (white line) is transmitted to the membranes (red), and back to mallet again. In the process, some of the energy is given to the strings (blue) and to the air (yellow), so that the final energy of the mallet is slightly less than the initial one.
References
[1] S.Bilbao. Numerical Experiments with Coupled Membranes and the Snare Mechanism, Proceedings of the 8eme Congrès Français d’Acoustique, Lyon, April, 2010.
[2] A. Torin, B. Hamilton and S. Bilbao. An Energy Conserving Finite Difference Scheme for the Simulation of Collisions in Snare Drums, Proceedings of the International Conference on Digital Audio Effects, Erlangen, Germany, 2014. Download paper
[3] S. Bilbao, A. Torin, and V. Chatziioannou. Numerical modeling of collisions in musical instruments, Acta Acustica united with Acustica, 101(1):155–173, 2015.
[4] A. Torin. Percussion instrument modelling in 3D: Sound synthesis through time domain numerical simulation, Ph.D. Thesis, University of Edinburgh, 2016.